Le nombre d'or
 Avez-vous déjà observé le coeur d'un tournesol ? Cela donne presque le vertige, tant on y distingue de spirales enchevêtrées. Sur une pomme de pin ou un ananas, les écailles dessinent aussi des spires régulières et entrecroisées ; et nombreuses sont les plantes dont les feuilles s'enroulent en hélice autour de leur tige, de même que les pétales autour du coeur. Même les «yeux» des pommes de terre, les germes qui donneront les bourgeons, sont disposés ainsi.
Avez-vous déjà observé le coeur d'un tournesol ? Cela donne presque le vertige, tant on y distingue de spirales enchevêtrées. Sur une pomme de pin ou un ananas, les écailles dessinent aussi des spires régulières et entrecroisées ; et nombreuses sont les plantes dont les feuilles s'enroulent en hélice autour de leur tige, de même que les pétales autour du coeur. Même les «yeux» des pommes de terre, les germes qui donneront les bourgeons, sont disposés ainsi.
Bref, le monde végétal est littéralement envahi par les spirales ! Constatation banale ? Bien plus que cela. Car, à les regarder de plus près, on s'aperçoit qu'elles partagent toutes une étrange prédilection pour des nombres mathématiques remarquables... Si remarquables même qu'ils fascinent depuis des siècles des bataillons de botanistes, de physiciens, de chimistes et de mathématiciens !
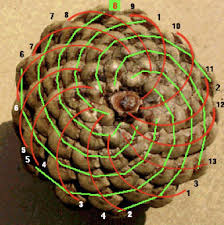
Pour accéder à ce mystère, il suffit d'avoir sous la main une pomme de pin et de savoir compter. Au premier regard, l'oeil est attiré par deux familles de spirales parallèles que forment les écailles ; ces spirales, appelées «parastiches», sont enroulées les unes dans le sens des aiguilles d'une montre, les autres en sens opposé. Comptons-les : on en trouve 5 dans un sens et 8 dans l'autre ; ou 8 et 13 comme chez l'ananas.
Pour un tournesol, on dénombrera 34 et 55 parastiches, ou même 89 et 144. En renouvelant ces comptages sur des plantes différentes, on comprend vite que ces nombres de parastiches ne doivent rien au hasard... En effet, ils ont tous en commun d'appartenir à une célèbre «suite» mathématique, la suite de Fibonacci (un mathématicien italien du XIIIe siècle). La recette de cette suite est on ne peut plus simple : chaque nombre est la somme des deux précédents. Les deux premiers éléments de la suite étant 0 et 1, cela donne : 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144...
Or, cette suite jouit d'une propriété très remarquable : au fur et à mesure que les nombres croissent, le rapport entre deux termes successifs tend vers le nombre d'or, véritable star des mathématiques. Nombre d'or que l'on retrouve, comme par hasard, quand on se penche sur la géométrie des plantes spiralées...
Le nombre d'or, t = (1 + v5)/2, soit 1,618..., est doué de tant de propriétés mathématiques et géométriques que, depuis des millénaires, il fascine les mathématiciens.
Son histoire commence même avant celle des mathématiques, puisqu'on le retrouve dans la grande pyramide de Gizeh. Au IIIe siècle avant J.-C., Euclide lui fait la part belle dans ses Eléments, fondateurs de la géométrie : il décortique certaines de ses propriétés, l'utilise comme premier exemple de résolution d'une équation du second degré et montre aussi que le rapport du côté du pentagone à sa diagonale est égal au nombre d'or.
Les anciens Grecs, qui vouaient un culte aux nombres et aux figures géométriques parfaites, avaient un faible pour t, qu'il avaient aussi baptisé «divine proportion», et «nombre de Phidias» (le plus grand sculpteur de la Grèce antique, auteur des frises du Parthénon).
 Au Moyen Age, le pentagone est utilisé dans les motifs des vitraux de cathédrale, et les maîtres des corporations se transmettent le secret de sa fabrication au compas, qui fait intervenir le nombre d'or.
Au Moyen Age, le pentagone est utilisé dans les motifs des vitraux de cathédrale, et les maîtres des corporations se transmettent le secret de sa fabrication au compas, qui fait intervenir le nombre d'or.
En 1509, pour le démythifier et lui donner des bases mathématiques, un traité illustré par Léonard de Vinci, baptisé De divina proportione, lui est consacré.
Le nombre d'or s'écrit aussi (entre autres...) :
t = 1 + 1/t = 1 + 1/(1 + 1/t) = 1 + 1/[1 + 1/(1 + 1/t)] =...
t = 1 + vt = 1 + v1 + vt = 1 + v1 + v1 + vt = ...
Quant à l'angle d'or, f, il est simplement égal à
360°/(1 + t), soit 137,5°.


Contribuez par vos questions et vos commentaires à l'échange d'informations amorcé par cet article (ou vidéo).
Partagez aussi votre savoir, nous restons à l'écoute !