Cathédrale gothique et pyramide d’Égypte
- Dossier : Énigmes de l'Histoire
- Imprimer l'article
Par Léon Goudallier, pour la revue Cosmos (nº 1280 et 1281, août 1909).
Lien pour accéder au document original en version PDF : http://www.inmyst...ale-gothique-et-pyramide-d-egypte-par-leon-goudallier.html
 A première vue, le rapprochement de ces deux monuments ne semble devoir être qu'une source d'antithèses; or, toute paradoxale que puisse paraître la proposition, il ne sera ici question que d'analogies. Dans une étude aussi ingénieuse que documentée, M. Knauth, architecte de la cathédrale de Strasbourg, a démontré que, sous une apparence absolument différente la basilique confiée à ses soins et la grande pyramide d'Egypte, dite de Chéops, ont été conçues d'après une formule identique [1].
A première vue, le rapprochement de ces deux monuments ne semble devoir être qu'une source d'antithèses; or, toute paradoxale que puisse paraître la proposition, il ne sera ici question que d'analogies. Dans une étude aussi ingénieuse que documentée, M. Knauth, architecte de la cathédrale de Strasbourg, a démontré que, sous une apparence absolument différente la basilique confiée à ses soins et la grande pyramide d'Egypte, dite de Chéops, ont été conçues d'après une formule identique [1].
Nous négligeons de parti pris les observations historiques et les considérations artistiques de ce travail, malgré le très réel intérêt qu'elles présentent, pour n'en consigner ici que les traits mathématiques essentiels.
« Des proportions en architecture s’établissent d’abord sur les lois de la stabilité, et les lois de la stabilité dérivent de la géométrie. Un triangle est une figure entièrement satisfaisante en ce qu’elle donne l’idée la plus exacte de la stabilité. Les Égyptiens, les Grecs sont partis de là, et, plus tard, les architectes du moyen âge n'ont pas fait autre chose. C‘est au moyen des triangles qu‘ils ont d’abord établi leurs règles de proportions, parce qu'ainsi ces proportions étaient soumises aux lois de la stabilité..... Les triangles acceptés par les architectes du moyen âge comme générateurs de proportions sont : 1º le triangle isocèle rectangle; 2º le triangle, dit isocèle égyptien, c’est-à-dire dont la base se divise en quatre parties, et la verticale tirée du milieu de la base au sommet, en deux parties et demie; 3º le triangle équilatéral [2]. »
On peut comprendre ces trois principes sous le nom de triangulature. En recherchant quelle méthode eurythmique a présidé à la construction de la cathédrale de Strasbourg, M. Knauth a constaté que, conformément aux règles suivies par les maîtres d’œuvre du moyen âge, tous les points architectoniques caractéristiques sont répartis d'après des rapports géométriques déterminés; les différentes projections montrent, tant en plan qu'en élévation, l'application d'une même figure géométrique simple et fondamentale.
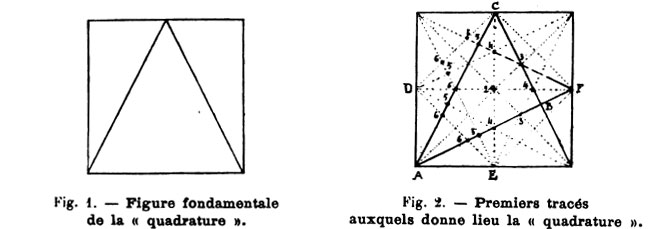
Toutes les proportions de l'édifice s'y ramènent ; cette figure est le carré [3] dans lequel est inscrit un triangle isocèle dont la base et la hauteur sont égales au côté du carré (fig. 1). En répétant ce triangle sur les quatre côtés du carré, on obtient l'octogone étoilé (fig. 2). Du plan d'ensemble jusqu'aux détails, cette formule et ses dérivés animent l'œuvre tout entière; entre toutes les parties du vaisseau s'établissent un enchaînement logique, d'étroites relations et de précieuses proportions.
Cette méthode géométrique offre, en outre, dans le domaine arithmétique, l‘avantage d’un système de division aussi peu compliqué que possible; il est donné par les intersections des lignes des triangles, qui se coupent les unes les autres dans le rapport des nombres 2, 3, 4 et 5.
Il convient de remarquer que le triangle rectangle A B C a pour côtés 3, 4 et 5 et n'est autre ainsi que le triangle appelé pythagoricien par Viollet-le-Duc [4].
En joignant entre eux les sommets des quatre premiers triangles, on obtient, placé diagonalement et inscrit dans le carré primitif, un deuxième carré. On y trace quatre triangles comme dans le premier, et les nouvelles intersections déterminent la série des nombres de 6 à 10.
Que si, par les points d’intersection des obliques, l‘on mène des parallèles aux côtés du grand carré, celui-ci se trouve divisé en un groupe de carrés plus petits qui se peuvent décomposer de la même manière [5].
A ce système non seulement ingénieux, mais encore admirablement souple, M. Knauth a donné le nom de quadrature.
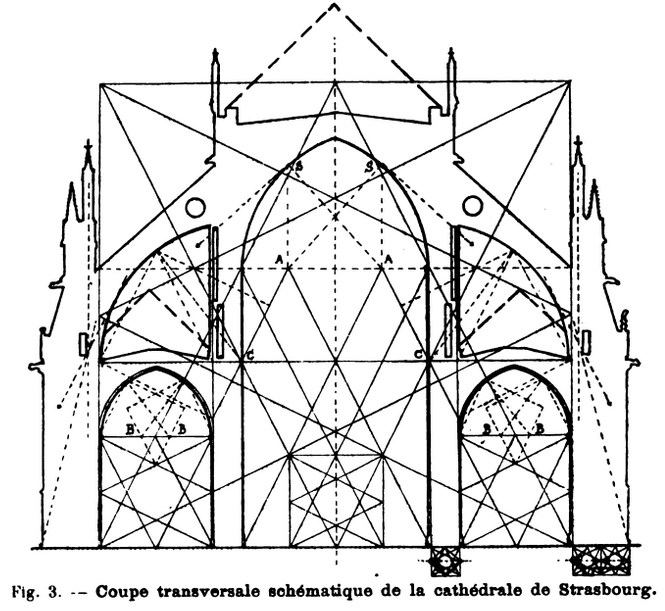
La coupe transversale est sans contredit l’élément fondamental de l'édifice qui nous occupe (fig. 3). On pourrait, ce semble, en trouver de façon approchée l'unité de mesure dans la centième partie de l'espace compris entre l'aplomb intérieur des contreforts et considéré comme le côté d’un carré où s’inscrit le monument. Dans ces conditions, la largeur prise entre piliers est de 40 unités pour la grande nef, de 30 unités pour chacun des bas côtés, y compris l’épaisseur des piliers de la nef; d’où un rapport de 3 à 4 et à 3. Les piliers de la nef sont avec la largeur des bas côtés dans un rapport de 6 à 24 unités (6 + 24 = 30), soit de 1 à 4. Quant aux contreforts, ils valent le double des piliers de la nef, soit 12 unités.
La hauteur comporte des rapports rationnels du même genre. Du sol jusque sous l’arête de la moulure du triforium, on compte 40 unités, donc mesure égale à la largeur de la grande nef ; du triforium au niveau de la naissance de la voûte, exactement 20 unités ; au total, la hauteur de la grande nef, du sol à la naissance des voûtes, vaut 60 unités, en rapport avec la largeur comme 3 est à 2. Du sol à la naissance des voûtes des bas côtés, il y a 24 unités, soit la largeur même de ces bas côtés.
Les procédés sont identiques pour le tracé des arcs. Placé sur la ligne de naissance des voûtes, le centre est au quart de cette ligne en A pour la grande nef, sur un point de huitième division en B pour les bas côtés et en C pour les arcs-boutants. Le point C est au niveau du dessous de la moulure du triforium envisagée plus haut.
 En plan, en élévation géométrale, aux travées de la nef, aux fenestrages des bas côtés, M. Knauth applique avec succès la méthode qu'il expose. Pour y parvenir, ses tâtonnements ont été plus ou moins longs, mais partout il a dû rejeter les tracés de la triangulature pour constater l‘emploi de la seule quadrature [6].
En plan, en élévation géométrale, aux travées de la nef, aux fenestrages des bas côtés, M. Knauth applique avec succès la méthode qu'il expose. Pour y parvenir, ses tâtonnements ont été plus ou moins longs, mais partout il a dû rejeter les tracés de la triangulature pour constater l‘emploi de la seule quadrature [6].
Toutefois, les deux systèmes ne sont point complètement étrangers l‘un à l‘autre, et le premier se révèle dans le second au moyen d’une construction très simple (fig. 4). Si le point A décrit autour de B une circonférence, de même C autour de D et E autour de F, ces révolutions déterminent autour de B les points d’intersection D, G, H. F, I, K, qui, joints entre eux et avec le centre B, donnent le triangle équilatéral et l’hexagone, éléments de la triangulature.
D'autre part, on peut remarquer que la circonférence dont D est le centre coupe le côté DE du triangle en L; en faisant tourner le point L autour de E, la nouvelle circonférence coupe les ligues CE et EM aux points N et 0; on trouve les proportions :
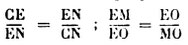
Ces divisions en moyenne et extrême raison, que Lucas Pacioli appelait divina proportione, ont de tous temps été l’objet d’une étude approfondie de la part des historiens d‘art; d'aucuns [7] y ont voulu reconnaître, qui l‘universelle loi de proportions des créations de la nature, qui l'incontestable base eurythmique des constructions de l'Égypte et de la Grèce.
[ Quoi qu'il en soit, l'on s‘accorde généralement à voir dans la nature le modèle permanent des arts. A suivre la filiation logique et harmonieuse des tracés géométriques de triangulature et de quadrature, on est amené à considérer ces principes comme empruntés à la nature elle-même, car on les retrouve dans les phénomènes de la cristallisation. Les anciens maitres d’œuvre n’ont obéi dans leurs méthodes de proportions qu'à une loi géométrique de la nature que M. Knauth formule ainsi : Les lois de proportions de l’architecture médiévale sont les lois géométriques de la cristallisation. ]
C‘est le principe de la quadrature que l’on découvre. avec quelques complications, il est vrai, dans la pyramide de Chéops, qui, près de Giseh, surgit au-dessus du sol comme la partie supérieure d‘un gigantesque octaèdre a demi ensablé. De l'aveu unanime des égyptologues, la grande pyramide. masse imposante s’il en fut, n‘est pas seulement, la plus ancienne et la plus achevée des constructions de ce genre, elle leur a encore servi de type.
Les plans latéraux de la plupart des pyramides présentent une inclinaison d‘un peu plus de 51º; cet angle constant implique entre la base et la hauteur un rapport précis, qui résulte soit d'une règle esthétique, soit de certaines prescriptions religieuses; à l‘intérieur de la pyramide, la pente des allées d’accès est comprise entre 26º et 27º.
Temple, asile de mystères cultuels, obstacle contre les sables, dépôt d'archives scientifiques, observatoire ou tombeau, la pyramide nous étonne par ses dimensions colossales et reste l’une des merveilles du monde. Le carré de sa base couvrait à l’origine une surface de 54 223 m2, sa hauteur était de 147,70 m et son volume de 2 669 593 m3. Aujourd’hui son revêtement primitif et son sommet ont disparu; de ce fait, sa superficie est réduite à 51 526 m2 et son volume á 2 473 248 m3 (fig. 5).
Des allées étroites et basses, deux chambres dans le corps de l’édifice et une troisième au-dessous du niveau du sol en constituent toute la distribution intérieure. La pente des allées correspond ici en moyenne a 26º34'; c'est précisément l’angle constant des diagonales d‘un rectangle dont la base est double de la hauteur et par conséquent l‘angle même compris entre le côté du triangle et celui du carré dans la quadrature (fig. 6).
Sans donner les mesures exactes de ces chambres et allées, on peut noter combien dans le carré OBDE le nombre 5 joue un rôle important; les points d’intersection des obliques déterminent les longueurs et embranchements d’allées d’après la division par 5; la pyramide est elle-même une figure stéréotomique qui comporte 5 faces et 5 pointes; la chambre centrale repose sur la cinquantième assise et ses parois sont formées par 5 blocs de granit ; son côté égale le cinquième du carré qui sert de point de départ à ces constatations.

Après les travaux du colonel Howard Vyse et de John Taylor, Piazzi Smyth fit d’autres recherches. A l’entrée de l’antichambre du tombeau royal se voit, au milieu d’une dalle de granit, un bouton rond qui fait saillie du cinquième de son épaisseur. Smyth y prétend trouver l’unité de mesure du maître d'œuvre de la pyramide; il appelle mètre pyramidal le quintuple de l’épaisseur de ce bouton, soit une mesure de 0,6356 m, et pour ce mètre il adopte une division en vingt-cinq pouces de pyramide; ce détail mystérieux aurait donc une épaisseur de cinq pouces et une saillie d’un pouce. « Il est à peine douteux, écrit Smyth, que cette mesure ait servi d‘unité au constructeur aussi bien dans son projet qu’à l'exécution, car toutes les mensurations d'allèes et de chambres donnent lieu aux plus surprenantes relations, si elles sont effectuées au moyen de cette mesure. » Or, par la plus invraisemblable des coïncidences. le mètre pyramidal représente exactement la vingt-millionième partie du diamètre terrestre. Ce dernier a 12 712 178 mètres [8]. Le mètre pyramidal vaut donc 0,6 356 089 mètre.
Devant un résultat aussi extraordinaire, les contradicteurs n'ont pas manqué a Smyth; les uns lui objectaient que ce n'était là que jeu du hasard; d'autres mettaient en doute l'exactitude de ses relevés.
M. Knauth a pris soin de montrer que le calcul confirme de tous points les assertions de Smyth, il procède comme il suit (fig. 7).
Il part directement de la mesure exacte du globe et d'une circonférence A tracée avec un rayon de 100 mètres pyramidaux, soit 63,56 m; concentriquement à la circonférence A sont tracées les circonférences B D E dont les rayons sont entre eux dans les proportions suivantes :
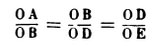
Tangents à la circonférence D sont menés les côtés du carré F G H I, dont les côtés F I et G H sont prolongés jusqu’à leur rencontre avec la circonférence E en K et M. On peut écrire :
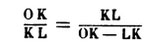
Les triangles C N L et R Q L offrent la même proportion.
Le double triangle C N P répond aux dimensions connues de la grande pyramide; les deux côtés qui en forment le sommet sont tangents a la circonférence A1, dont le rayon a pour longueur 100 mètres pyramidaux et dont le centre est placé a la hauteur même du bouton mystérieux à l’entrée du tombeau royal. Les circonférences égales A et A1 de la coupe transversale font place dans la pyramide à une sphère d’égal rayon dont l’épaisseur est bien exactement le cent millième du diamètre terrestre. 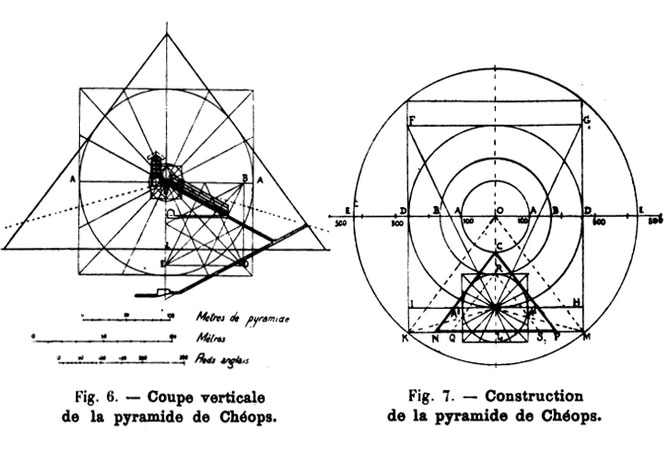
Passons de la construction graphique au calcul.
En prenant la ligne de base au-dessus de l’assise qui sert pour ainsi dire de socle à la pyramide, on obtient : pour le côté du monument, 365,2028 mètres pyramidaux, soit 232,1229 m; pour la hauteur totale 232,038 mètres pyramidaux, soit 147,4833 m; pour l'inclinaison des faces, un angle de 51°42’30".
D‘après ses relevés, le colonel Vyse accusait pour la base primitive 764 pieds anglais, mesure plus tard rectifiée à 761,70 pieds anglais, soit 232,16 m, et pour l’inclinaison des faces, dont il avait vu autrefois deux des pierres de revêtement encore en place, un angle de 51°50'.
Bref, opérations sur le terrain, construction graphique et calculs concordent de façon suffisante pour qu’on puisse admettre l'emploi du mètre pyramidal comme unité de mesure.
De leur côté, Taylor et Smyth, s‘appuyant sur leurs mensurations et surtout sur l‘inclinaison du revêtement, ont ainsi établi le rapport du double de la ligne de base à la hauteur :
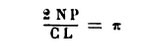
Cette réalisation approchée de la quadrature du cercle, problème qui a tant occupé les intelligences au cours des siècles, n'est pas la moins curieuse des particularités qui distinguent le monument égyptien. Taylor a même cru dans ce cas pouvoir déterminer 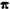 jusqu'à la cinquième décimale; il est toutefois permis de douter de l‘exactitude de ce résultat, car la mesure de l’angle à la base ne lui a été donnée que par le relevé d'une seule pierre du revêtement. Le sommet de la pyramide est ruiné, des tassements ont pu se produire, et l'on ne peut connaître rigoureusement la hauteur primitive. Il n'en reste pas moins remarquable d’obtenir ainsi pour
jusqu'à la cinquième décimale; il est toutefois permis de douter de l‘exactitude de ce résultat, car la mesure de l’angle à la base ne lui a été donnée que par le relevé d'une seule pierre du revêtement. Le sommet de la pyramide est ruiné, des tassements ont pu se produire, et l'on ne peut connaître rigoureusement la hauteur primitive. Il n'en reste pas moins remarquable d’obtenir ainsi pour 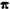 une évaluation exacte jusqu’à la troisième décimale exclusivement.
une évaluation exacte jusqu’à la troisième décimale exclusivement.
L‘axe de l‘allée qui descend sous la pyramide est à peu de chose près dirigé vers le pôle de la voûte céleste; John Herschell en avait fait l‘observation. On constate que la base de la pyramide est de 365,2028 mètres de pyramide; c'est aussi le nombre de jours que met la terre à accomplir sa révolution autour du soleil. Le mètre pyramidal est, tout comme notre unité de mesure du système métrique, emprunté à l’une des dimensions du globe terrestre [9].
Enfin, Smyth ajoute que le pouce pyramidal, vingt-cinquième partie du mètre pyramidal, ne diffère du pouce anglais actuellement en usage que d’environ un millième.
Quoi qu‘on puisse penser de ces divers résultats, il semble difficile de n'y voir que le caprice du hasard.
***
On se rappelle qu‘en appliquant à la cathédrale de Strasbourg la quadrature, un nombre de cent unités avait été adopté comme côté du carré où s’inscrit la coupe transversale. Ces cent unités représentent une moyenne de 35,53 m. Une unité vaut donc 0,3553 m. Mais si cette mesure règle bien, comme on l‘a vu, maint détail, elle ne concorde en aucune façon ni avec le pied autrefois employé ni avec l’unité de mesure de la grande pyramide.
Il est à croire, en effet, que l’architecte gothique n'a pas pris cette mesure pour point de départ.
Les hommes de métier savent combien est délicat l‘établissement rigoureux sur le terrain d’un angle droit. L’une des plus sûres méthodes pour y réussir est de se servir à cet effet du triangle dont les côtés sont 3, 4 et 5.
Il est fort probable que les anciens maîtres ne sont point partis du côté du carré, mais plutôt du côté du triangle inscrit; de la sorte, on obtient des résultats qui se rapportent étroitement aux objets de cette étude.
Appelons q le côté du carré et d le côté du triangle inscrit; ainsi :
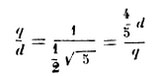
Le côté du carré étant de 35,53 m, on a pour le coté A B du triangle A B C (fig. 2) :
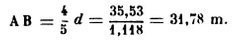
Or, cette mesure vaut précisément cinquante mètres pyramidaux.
Passons aux applications.
Le calcul donne :
1º Entre les lignes de construction :
- a) Pour la largeur de la grande nef, 14,212 m
- b) Pour les piliers, 2,132 m
- c) Pour la largeur de chaque bas-côté, 8,527 m
Au total, 35,53 m.
2º D'où il vient, dans œuvre :
- a) Pour la largeur de la grande nef, 13,964 m
- b) Pour les piliers, 2,380 m
- c) Pour la largeur de chaque bas-côté, 8,279 m
Au total, 35,282 m.
Les relevés montrent que la largeur de la grande nef dans œuvre varie entre 13,955 et 14,016, celle des bas-côtés entre 8,253 et 8.302 m, tandis que les piliers mesurent à peu de chose près 2,380 m, variations uniquement dues aux mouvements de l’édifice depuis sa construction.
D'après les observations de M. Knauth, la même unité de mesure, empruntée au globe terrestre, a donc été employée à la pyramide de Chéops et à la cathédrale de Strasbourg, entière dans le premier de ces monuments, réduite a la moitié dans le second (0,6356 et 0,3178).
***
Devant ces concordances, on se prend tout naturellement à se demander si certains principes architectoniques remontant à la plus haute antiquité ne se sont pas perpétués par tradition à travers les âges. Par suite des fréquents arpentages nécessités par les crues du Nil, les Égyptiens étaient rompus aux levés de plans et aux tracés géométriques; les maitres d’œuvre gothiques ne leur étaient point inférieurs sur ces points; les merveilleux monuments de toutes dimensions qu'ils nous ont laissés le prouvent surabondamment.
Les règles mises en pratique ont-elles été gardées par les uns et les autres dans les ateliers de construction comme des secrets mystérieux? Autant de questions qu‘il est plus aisé de poser que de résoudre.
Ainsi réduit à ses seules données mathématiques, le travail de M. Knauth prend une apparence catégorique qu'il n‘a pas dans l’œuvre originale. L’éminent architecte ne tente pas de tirer de son étude des conséquences aussi absolues que téméraires. Il se borne seulement à souhaiter que le même procédé de mensuration soit appliqué à d’autres édifices du moyen âge. A l'avenir maintenant de nous apprendre si de nouvelles expériences viendront confirmer sa thèse.
Léon Goudallier.
Notes :
- [1] Das Strassburger Münster und die Cheopspyramide Rätsel der Baukunst, von Dombaumeister, J. Knauth. Strassburg. Broch. in-4º, 48 pages, 31 illustrations. — C. A. Vomhoff Verlag, Strassburg i. E. 1908. Voy. égal. la Revue alsacienne illustrée, nº2, 1907... [Lien à venir]
- [2] Viollet-le-Duc, Dict. raisonné de l'architecture française, t. VII, p. 534. Art. « proportion ».
- [3] Notons en passant que le carré était précisément la marque de l'atelier de Strasbourg. Nous devons les clichés des figures 1, 2 et 4 à la parfaite obligeance de M. le directeur de la Revue de l’Art chrétien.
- [4] Viollet-le-Duc. Entretiens sur l‘architecture, t. I. Neuvième entretien, p. 402 sq.
[5] Ces parallèles n‘ont pas été tracées ici pour ne point compliquer la figure. - [6] Il va sans dire que dans ses opérations M. Knauth a tenu compte des déformations produites par les mouvements de l'édifice au cours des siècles.
[7] Zeising, Schultz, etc. - [8] Valeur approché du diametre polaire.
- [9] Sur les relations de la pyramide de Chéops avec l'astronomie, voir l'Astronomie à travers les âges, par L.-M. Pioger, p. 88 sq. En ces pages sont résumés, avec l'autorisation de l’abbé Moigno, les travaux de Piazzi Smyth sur la grande pyramide.


Contribuez par vos questions et vos commentaires à l'échange d'informations amorcé par cet article (ou vidéo).
Partagez aussi votre savoir, nous restons à l'écoute !